Paul Hsieh's puzzles

Logical

Index: Set 2 | Set 1

Set #2

1. Suppose you have two permutation functions on the numbers from 0 to 255. The first, add1, adds 1 to the number if its between 0 and 254, and maps 255 back to 0 (so its an add by 1 modulo 256). The second, rol1, doubles numbers between 0 and 127, and takes a number x between 128 and 255 to 2*x-255 (so its a bit rotate left.) Can all permutations on the numbers 0 to 255 be generated from successive compositions of these functions? If so how?

2. * Given three binary inputs (a,b,c), two inverters and an infinite supply of and and or gates (and forks, for duplicating a result, but I suppose this is a given) construct a black box which has three outputs which are the inverse of three inputs (~a, ~b, ~c).

3. (Follow up to the above) True or false: If we can create 3 inverters from 2, then we can create n+1 inverters from n, and from induction that means we can create n+a from n, and thus n from 2.

4. Without using measuring instruments, what is the fairest way to have three people slice a pie into three portions? The conditions being that anyone might be forced to do the slicing and will be satisfied with either the piece they sliced or a "fair" portion of the remaining amount of pie. For example, with two people, one cuts, the other chooses. (Notice that for 3 people, if one cuts and another choses that piece and gets it if s/he wants, then the third person could be potentially unsatisfied since they may not be satisfied with a portion of the remaining amount.)

5. * (Follow up to the above) What if you had n people who wanted a fair portion of the pie?

6. Suppose that you have 3 men in front of you. One always lies, one always tells the truth and one might do either. They know which is which, but you do not. With 3 yes/no questions, determine which is which.

Set #1

1. You have two strings of rough non-countinuous composition (in other words these strings are not ideally uniform.) You know that each will take exactly half an hour to burn no matter which end is lit. How can you with only one match (which only sustains a flame for a few seconds) measure a time interval of 45 minutes?

2. There are 4 cards on a table. Each has a number on one side and a letter on the other. The cards show A,B,1 and 2. Which 2 cards would you turn over to test the rule that "All cards with a vowel on one side have an even number on the other"

3. Three men walk into a restaurant and each order the lunch special that costs $10. When they are ready to pay the $30, the owner of the restaurant pulls the waiter aside and says: "These three men are my friends. Give them $5 off the check". When walking towards the table, the waiter thinks: "$5 split between 3 men? Not easy. I'll give them each $1 and keep the last $2". He does so, everybody is happy. Tips and taxes aside, how much did each man pay?
   • Each man laid down $10.
   • Each gets $1 back.
   • Each has paid $9.
   • In all, they have paid 3x$9 = $27.
   • The waiter kept $2.
   • $27+$2 = $29.

   Where is the last dollar?

4. I ask you to shuffle a standard complete deck of playing cards (no jokers) thoroughly. Then I ask for them back (face down). Carefully examining the backs of the cards, I separate them into two piles. I then claim that, through the power of magic, I've made sure that the number of black cards in the first pile is the number of red cards in the second pile! The explanation starts as follows: "While pretending to examine the backs of the cards, I was simply ..." Can you complete this explanation?

5. Here are two problems pertaining to geostationary orbits. The goal is not simply to answer the questions, but to explain your answers in everyday language.
   1. As part of a strategic defense proposal, a prominent politician proposes to place a defensive satellite in geostationary orbit directly over Washington DC. What's wrong with this proposal?

   2. A satellite in geostationary orbit appears to be in the same place in the sky all the time, because the satellite orbits the Earth at the same rate as the Earth rotates. And yet, every satellite in geostationary orbit goes around the Earth with respect to the stars once every 23 hours, 56 minutes and 4 seconds (give or take a few seconds), NOT 24 hours. How, then, can the satellite appear to be in the same place all the time?

   The answer to Question 1 does not depend upon the workability of any "Star Wars" device. And answering "It won't work" is not sufficient, because the problem already tells you that.

   The answer to Question 2 does not depend upon what a "few seconds" means

6. What is wrong with the idea at this site?

Mathematical

Now for the problems:

Index: Set 6 | Set 5 | Set 4 | Set 3 | Set 2 | Set 1

Set #6

1. Consider the following scenario. After waiting 1 second, two balls are placed in a bag, and one of the balls is immediately removed and set aside in a pile. Then after 1/2 seconds another two balls are placed in the and again one ball (from the bag, not necessarily from the two balls just placed) is immediately removed. This sequence is repeated after waiting 1/4, 1/8, ... etc. seconds. The question is, after 2 seconds, how many balls are in the bag? At any stage the number of balls in the bag is always equal to the number pulled out, so it would seem that there should be two infinite sets of balls -- thus there are an infinite number of balls in the bag. However, suppose we label the balls in the order in which they are placed in the bag, and remove them in exactly the numeric sequence of their labelling. Then the set of balls put into the bag are labelled {1, 2, 3 ...} but the balls taken out and sitting in the pile to the side is the sequence {1, 2, 3 ...}. That would suggest that every ball that goes in, eventually comes out.

   In other words, 0 = infinity. Explain what has gone wrong.

2. Lambert's W function is defined as follows: W(x)e^W(x) = x. Prove that lim_x->inf W(x) / (ln(x) - ln(ln(x))) = 1.

3. Suppose you are in the elevator of a 20 story building at the top floor. All of a sudden the elevator cable snaps, and the emergency brake completely fails (an insanely unlikely occurence) and the elevator proceeds to drop in a 20 story free fall. If you do nothing, the fall will kill you, so before the point of impact you consider possibility of jumping up from the floor of the elevator as hard as you can right at or possibly just before the point where the elevator finally hits the ground. Does this have any chance of working?

4. Suppose a bucket is floating in a bathtub filled with water, and in the bucket is a metal wrench. Now suppose we take the wrench out of the bucket and drop it into the bathtub so that it sink and is completely submerged. Does the water level in the bathtub raise, lower, or stay that same?

5. Suppose 100 prisoners are in a line. Each prisoner is given a hat, but are not allowed any form of communication after they are given the hats (no blinking morse code or anything like that). They are standing in a line facing front and can see all the hats of the others in front of them, but not their own or anyone behind them. They are told that the probability of the hat they are wearing being black is 2/3, and that the remaining hats are white and that each hat was independently randomly chosen with these odds. Now each prisoner will be called up in the order of the line starting with the one in the back (who can see 99 other hats in front of him/her), one by one is forced to guess which color the hat on their own head is. If they guess correctly they live, if they guess incorrectly they are executed on the spot right then and there. As the procedure progresses the others can hear the guesses of those behind him/her and whether or not they guessed correctly.

   Ok, assuming that the prisoners are allowed to collude and strategize before they are given their hats (they know of the pending situation before it takes place, but cannot communicate at all once the hats are given out), what should they do to maximize their probability of their own survival? What should they do to maximize the number of surviving prisoners (is this the same question)? And assuming there is a difference in the two strategies, what if some of the prisoners (with probability p) decides to be selfish and go with a selfish strategy instead of strategy which maximizes the number of survivors?

Set #5

1. An enemy submarine is travelling along a ruled line starting at an unknown integer offset at time 0, and moving at an unknown constant speed of a integer displacement per minute. Now suppose we have a missile system with unlimited ammunition that can strike at any single integer offset (but just one at a time) on this line at any given moment. Is there a way to strike the submarine with a missile in a finite amount of time?

2. 400 pirates plunder a ship and loot 100 gold coins. Now they must split the coins among them. To do this, they always follow this procedure: One pirate makes a proposal about how to split the gold. Then they all vote whether or not to accept this distribution of the booty. If the proposal takes at least half (not half+1) the votes then the proposal passes, the coins are given as the proposal says and they are done. But if the proposal fails the vote, then the stupid pirate that made the proposal is killed, and the next one makes his proposal (they all know their turn a priori, that is to say, there is a ranking amongst them). Dead pirates don't vote. Now, every pirate has the same criteria when voting for or against a proposal : 1) He must do what he can to live, 2) If he is sure he'll live, than he tries to take as many gold coins he can and 3) If the first 2 criteria are satisfied, then he tries to kill as many of the other pirates he can. A gold coin can't be cut into smaller pieces and all these pirates are people with logic enough to make the right decisions and they all know that about each other. What is the most logical way for the gold coins to be split, and how many pirates survive this ritual?

3. What has gone wrong here:

   

4. Suppose we have a sequence of n integers {a₀, a₁, ... a_n-1} each from the range [0, 2ⁿ-1]. Give a simple function that returns a specific integer in this range which in not equal to any of the a_i. (Computer programming interpretation: write a function using just arithmetic and logic operation which do not use control structures like "if" or C's "? :" operator or Perl's "when" clause or loops.)

5. Does there exist a real valued function that grows faster than any polynomial but not as fast as any monotonically increasing exponential? If so, give an example of such a function. That is to say, find a function f(x), if it exists, such that:
   • For all integers n > 0, there exists an L such that f(x) > xⁿ for all x > L.
   • For all real values e > 0, there exists an L such that (1+e)^x > f(x) for all x > L.

6. ** Generalization of above. Suppose we have two sets of postive, monotonically increasing functions, F and G and that for any function f in F and function g in G we have the following:

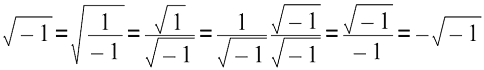
   lim_x->inf  f(x)/g(x) -> 0

   Does there exist a function h, such that:

   lim_x->inf  f(x)/h(x) -> 0 and lim_x->inf  h(x)/g(x) -> 0 ?

   If so, construct the function h(x).

Set #4

1. The band U2 whose 4 members are Bono, Edge, Larry and Adam need to get to the stadium to perform. On the way there they encounted a bridge that they need to cross to get there. But its pitch black out, they have one flashlight, and the bridge can only support two at a time. Its too treacherous to cross the bridge without the flashlight, so no journeys across the bridge are made without the flashlight. Now they are in kind of a hurry, so they need to get across as fast as possible. It turns out that they walk at different speeds. By themselves Bono, Edge, Larry and Adam can cross the bridge in 1 minute, 2 minutes, 5 minutes and 10 minutes respectively. So if two are walking across, their combined speed is that of the slower of the two. The question is, how can they cross the bridge, and how do they do it in the least amount of time? (related problem)

2. * Just for fun a gambler approaches you and asks you if you want to make an even bet with him. Sure you say, being a gambler yourself. Now he says he's going to pick two different random numbers from a distribution not known to you. He will then write the two numbers of two small pieces of paper and put each one in each of his enclosed hands. You then pick a hand and he will reveal the number in that hand. You then place your money on which hand you think contains the larger number. He will match your money, betting on the other hand (regardless of whether or not you chose correctly -- this is a precondition), the numbers will then be revealed and whoever was right keeps the sum of the money. You only get one shot at this, and the bet is $10,000. The question is, is there a strategy to beat 50:50 odds and if so how? (This is probably the hardest problem on the page.)

3. * Bernie and Kevin are walking by a swamp where they happen upon a talking frog. The frog says aloud "I'm thinking of a pair of numbers from 3 to 97" (inclusive). The frog jumps onto Bernie's shoulder and says "The sum of the two numbers is ..." then whispers the sum of the two numbers into Bernie's ear. The frog then jumps to Kevin's shoulder and says "The products of the two numbers is ..." the whispers the product of the two numbers into Kevin's ear. The frog then jumps back into the swamp, never to be seen or heard from again.
    Bernie and Kevin stare at each other not knowing what to make of it, but for a moment not saying a word. Then Bernie says "Well I don't know what the numbers are but at least I know you don't know what the numbers are either". Kevin thinks for a moment and says "Aha! In that case I know what the number are!". At first Bernie is perplexed, but then responds "Oh I see! Then I know what the numbers are as well!"
    What are the numbers?

4. A duck is swimming in the center of a perfectly circular pond, and a fox is on the land at the very edge of the pond. The fox is hungry and wants to eat the duck, but it cannot swim. The duck wants to get out of there but needs to reach land in order to be able to fly away. If the duck swims at 1 meter per second, and the fox can run around on land at 4 meters per second, can the duck somehow escape?

5. Explain this:

   

6. Create a directed network on 10 vertices such that the path length between any two distinct points is at most 3, and each vertex has at most 2 outgoing connections.

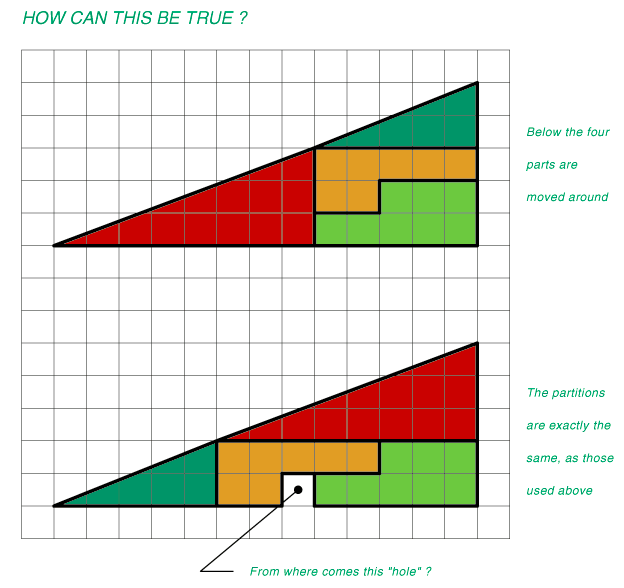
   If you are unfammilliar with the language used above: Place 10 points on plane, then draw unidirectional arrows connecting point pairs together (the arrows can overlap) such that each point has no more than 2 arrows coming out of it, and you can follow the arrows between the points such that at most 3 arrows need to be traversed to get between any pair of points.

1. Suppose we have a uniformly random input bit stream that we do not want to allow more than five 1 bits in a row to be output. To ensure decodeability we use the following scheme: we simply copy the input bits to the output bits, but as soon as the output stream receives five 1 bits in a row an additional 0 bit is sent. Under this scheme what is the expected asymptotic percentage increase in the length of the stream from input to output?

2. Suppose we have a pair of lines in regular 3 dimensional space and a pair of line segments of length a and b on the lines (one on each.) By joining all the vertices of the line segments we get a pyramid. In fact, if the lines don't intersect and aren't exactly parallel you will have a pyramid of non zero volume no matter where on the lines the line segements are placed. What positioning of the line segments maximizes the volume of the pyramid?

3. Suppose we have 100 lockers which start all closed. You start at one end and open every locker one by one. You then return to that end and then starting with the second locker close every other locker. You then return to that end again and starting from the third locker change the state (if it is open close it, if it is closed open it) of every third locker. Then every fourth, every fifth and so on. You do this for 100 passes. What is the state of each locker after you are done?

4. Suppose we have n coconuts gathered by 5 primitive men that have agreed to share them equally but who do not trust each other. They all go to sleep, but in the middle of the night the first guy wakes up divides the coconuts by 5 and hides his share of one fifth in his hut but there was a remainder of one coconut left after division so he gives it to a monkey that happens to be around (and awake) then he goes back to sleep. The second guy wakes up and divides the remainder of the pile into 5 and hides his share, but again there was a remainder of one that he gives to the same nearby monkey (which is still awake) before going back to sleep. This same procedure occurs for each of the remaining 3 primitive men (including the last one because nobody was a aware of the others' insomnia.) Assuming that the monkey gets 5 coconuts (there was always a remainder of 1 after dividing the piles by 5) what is the minimum number of coconuts that they could have started with?

5. Suppose you and nineteen other fine up standing citizens are captured by terrorists and each of you is put into an room (isolated from the others) with a button and a timer which is counting down starting from 10 minutes. You are told that if you press the button you will die instantly, but everyone else who does *not* press the button will be allowed to live and set free, however, if noboy presses the button, everyone will die. Given that the terrorists will keep their word, how would you decide on whether or not to press the button?

6. Out of the set of integers 1,...,100 you are given ten different integers. From this set, A, of ten integers you can always find two disjoint non-empty subsets, S & T, such that the sum of elements in S equals the sum of elements in T. Note: S union T need not be all ten elements of A. Prove this.

1. A boy, a girl and a dog go for a 10 mile walk. The boy and girl can walk at 2 mph and the dog can trot at 4 mph. They also have a bicycle which only one of them (including the dog!) can use at a time. When riding, the boy and girl can travel at 12 mph while the dog can pedal at 16 mph. What is the shortest time in which all three can complete the trip (and how do they do it)?

2. Four bugs are placed at the corners of a square. Each bug walks always directly toward the next bug in the clockwise direction. How far do the bugs walk before they meet?

3. Suppose you had an infinite supply of equally sized, rigid, playing cards. You pile them on the edge of a table by placing them one by one on top of each previously placed card (each also only touching the previously placed card) so as to have the total structure lean as far off the edge as possible without any other support (besides themselves and gravity) and without falling off the edge. If you are further subjected to the restriction that each card only touches the previously placed card and that you may not disturb any card if subsequent cards have been placed, how far over can you go?

4. In trapezoid ABCD, with AB parallel to CD, M is the midpoint of AD. Find the ratio of the area MCB to the area of the trapezoid ABCD. (from Mayhem)

5. A triangle with inradius r and area K are given. Prove that 9r*r/K <= tan(A/2) + tan(B/2) + tan(C/2). (from Mayhem)

6. Suppose you have milk and coffee in equal quantities in two different cups. You pour some of the milk into the coffee then pour back some of the mixture back into the milk cup so that there is the same total amount of liquid in both cups once again. Is there more, less or an equal amount of milk in the coffee cup than there is in the milk cup?

1. Let's say you and I play a simple game. I have a circular table and an unlimited supply of identically shaped, centrally symmetric, Cuban cigars. We each take turns placing a cigar on the table without disturbing any other cigars already there in the process and without overlapping any of the already placed cigars. The winner will be last person to successfully place a cigar on the table subject to the given restrictions. If I give you the option of going first, how would you play in order try and win?

2. I know 3 psychics. A fair coin is flipped and then hidden. Molly has an 80% chance of guessing the state of the coin (heads or tails), Spike has a 70% chance, while poor Waldo only has a 10% chance of a correct guess. What is the best scheme using all of these guesses to predict the state of the coin? What degree of accuracy does the best scheme give?

3. (Watch out, this question is very controversial.) On the game show "Let's make a deal", Monty Hall (the host) walks up to a contestant and gives them $100 unless they want to play "the three doors". The contestant usually turns down the money and plays "the three doors". Now behind one of the doors is an enormous cash-value grand prize, behind the other two are silly prizes such as a years supply of toilet paper or a goat. So Monty asks this same contestant to pick one of the three doors, which they do. Then, before opening the chosen door and revealing what's behind it, he opens one of the other doors which reveals one of the lesser prizes (let us assume that he always does this, and picks a random door when he has a choice except that he never inadvertently opens the door with the grand prize behind it). Monty then gives this contestant the option of staying with their chosen door or switching to the other door which still remains closed. The contestant then decides what to do and is rewarded with whatever prize is behind the door they finally chose. So the question is, should the contestant switch or stay?

4. Extended Monty Hall (I am daring to even go above Martin Gardner's head on this one.) Suppose that Monty has the option of not offering you the opportunity to switch (and therefore you are simply stuck with your choice whatever it is) and further suppose that you do not know beforehand whether or not Monty will offer to switch. Ok, the show is on a budget so Monty's primary objective is to not increase your odds of winning with his strategy versus any counter strategy you might come up with (Monty does know the position of the prizes beforehand). But Monty's secondary objective is to make the game as entertaining as possible by offering the switch as often as possible without compromising his primary objective. The question then is, what is Monty's strategy, and what is your best counter strategy?

5. Let's you and me play another game. This one is simple enough, tic-tac-toe n in a row. n is an integer greater than 1 and we'll play on an unbounded 2D grid, following the regular rules of tic-tac-tow. I allow m in a row, where m>n, to be as good as n in a row, i.e., you still win even if you get too many in a row. For what n can the second player force a win? (Hint/Note: It has been proven that tic-tac-toe 8 in a row is a draw, with best play from both sides.)

6. Ok, enough of these games. There are three people named Larry, Curly and Moe. One always tells the truth, one always tells a lie and the other gives unpredictable answers, but all of them can only answer yes or no questions (with yes or no). Like any classic Smullyan puzzle (from whom I believe this problem originates), the goal is to ask a certain number of questions to figure out who is who. In this case, the three know who is which and now you are allowed three yes or no questions (each directed to only one of the three at a time) to figure it out for yourself. How's do you do it?

7. * Let's say you have a table with 4 perfectly even table legs arranged in square positioning. I.e., on a flat floor the table sits perfectly flat. Now lets say that you have a floor that isn't quite flat. When you first place the table on the ground it wobbles because not all the legs touch the ground at once. Suppose that the floor is essentially unbounded and that from any given position you can drag the table in any direction (possibly requiring that you tilt the table so that only two of the legs are touching.) Can you always find a position on this floor such that the table does not wobble?

Hints

If you wish, you may submit solutions to me via email.

Credits

• William Wu's riddles
• Nick's Mathematical Puzzles
• Mathematical Mayhem (Two of the problems from set #2 were taken from here.)
• Theseus and the Minotaur
• Eric Weisstein's world of Mathematics
• Chris Long's Think and Derive Page
• Discover Games -- brain teasers
• Search for puzzles on Google
• Popcap -- Mind bending online game
• TEST YOUR I.Q.
• Stephen Magill Math Puzzles
• Purdue University's Problem of the Week