Paul Hsieh's real puzzle hints

Logical

• Suppose you have two permutation functions on the numbers from 0 to 255. The first, add1, adds 1 to the number if its between 0 and 254, and maps 255 back to 0 (so its an add by 1 modulo 256). The second, rol1, doubles numbers between 0 and 127, and takes a number x between 128 and 255 to 2*x-255 (so its a bit rotate left.) Can all permutations on the numbers 0 to 255 be generated from successive compositions of these functions? If so how?

- Can you produce the function x => (x xor 128)? Can you produce x => (x xor (1 shl n))?

- Can you create a permutation function which just swaps two values?

- Consider the functions: x => rol1(inc1(rol1(inc1(x)²⁵⁵))²)⁷ and x => inc1(rol1(inc1(rol1(x)))⁷)¹²⁸. Can these functions be composed to create generators for all other permutations?

• Given three binary inputs (a,b,c), two inverters and an infinite supply of and and or gates (and forks, for duplicating a result, but I suppose this is a given) construct a black box which has three outputs which are the inverse of three inputs (~a, ~b, ~c).

- For those interested in a paper and pencil proof: Consider the following statement: "Either two or three inputs are high". Can the truth value of such a logical statement be made from and's and or's of the inputs? What similar statements can be made and what are the implications of inverting them?

- For those who want to generate a computer solution: If we take the values 0xAA, 0xCC, 0xF0 and consider the nth bit of each, we see that all 8 combinations of 3 binary inputs are represented. That is to say, these numbers are independent representations of the three inputs. Now 0xAA & 0xCC = 0x88, which is a correct represenation of (a and b) if a is represented by 0xAA and b is represented by 0xCC. By starting with 0xAA, 0xCC, and 0xFF compute the space of values that can be obtained by ands, and ors. Then arbitrarily invert one of them and compute the new (possibly bigger) space that is obtained by ands and ors. Repeat the process again and see if the values 0x33, 0x55 and 0x0F are simultaneously in the space.

- Solution:

t3   = A and B and C
t23  = (A and B) or (B and C) or (A and C)
t123 = A or B or C

Then:

t01  = not t23
t1   = t123 and t01
t31  = t3 or t1
t02  = not t31
t0   = t01 and t02

We then compute:

A' = (t1 and (B or C)) or (t02 and B and C) or t0
B' = (t1 and (A or C)) or (t02 and A and C) or t0
C' = (t1 and (B or A)) or (t02 and B and A) or t0

• True or false: If we can create 3 inverters from 2, then we can create n+1 inverters from n, and from induction that mean we can create n+a from n, and thus n from 2.

- From your solution of the previous problem create a computer program that performs inv3(inout: a, b, c) using only two NOT operations. From here try to create an inv4(inout: a, b, c, d) using only AND, OR, copying and the inv3 function.

- Is it possible to work around the feedback problem?

• Without using measuring instruments, what is the fairest way to have three people slice a pie into three portions? The conditions being that anyone might be forced to do the slicing and will be satisfied with either the piece they sliced or a "fair" portion of the remaining amount of pie. For example, with two people, one cuts, the other chooses. (Notice that for 3 people, if one cuts and another choses that piece and gets it if s/he wants, then the third person could be potentially unsatisfied since they may not be satisfied with a portion of the remaining amount.)
• * (Follow up to the above) What if you had n people who wanted a fair portion of the pie?

- Think of the pariticipants, as slicers, and complainers. The object is to reduce the complainers.

- Arrange the people in a line. Have the first person cut off a "fair" slice of the pie, then proceed down the line giving each person the option of judging the slice to be a fair portion for someone else to have or not. As soon as one person says its unfair (because they think its too big), have them slice that slice of pie smaller so that it is "fair", and continue down the line with the same judging and iterative slicing until the end of the line has been reached. The last person that does slicing is stuck with that piece. Proceed by induction.

• Suppose that you have 3 men in front of you. One always lies, one always tells the truth and one might do either. They know which is which, but you do not. With 3 yes/no questions, determine which is which.

- How much information can you get in the first question? Can you determine with one question at least one person that is either the truth teller or liar?

- Is it sufficient to have only determined one person's identity after two questions?

• You have two strings of rough non-countinuous composition (in other words these strings are not ideally uniform.) You know that each will take exactly half an hour to burn no matter which end is lit. How can you with only one match (which only sustains a flame for a few seconds) measure a time interval of 45 minutes?

- If you burn a string at both ends, it will completely burn in 15 minutes.

- 30 + 15 = 45. So burn one string completely, and when its done burn both ends of the other. Since you have only one match, and the only flame available at the end of the first half hour will be on the end of the first string we must therefore light the two ends of the second string with the final flame of the first string. So form a ring with the second string, attach it to the end of the first, and light the other end of the first. The whole thing will completely burn in 45 minutes.

• There are 4 cards on a table. Each has a number on one side and a letter on the other. The cards show A,B,1 and 2. Which 2 cards would you turn over to test the rule that "All cards with a vowel on one side have an even number on the other"

- How does turning either B or 2 card help test the hypothesis?

• Three men walk into a restaurant and each order the lunch special that costs $10. When they are ready to pay the $30, the owner of the restaurant pulls the waiter aside and says: "These three men are my friends. Give them $5 off the check". When walking towards the table, the waiter thinks: "$5 split between 3 men? Not easy. I'll give them each $1 and keep the last $2". He does so, everybody is happy. Tips and taxes aside, how much did each man pay?

- Is the original $30 price even a factor in the problem?

- The original $30 is first partially reimbursed ($3 dollars is given back) and the remaining balance of $27 is paid by the men, and received by the waiter ($2) and the restaurant ($25). I.e., $27 = $2 + $25. Adding $27 and $2 is incorrect since its at best counting the waiter's tip twice and ignoring the payment to the restaurant (and thus is not actually measure of anything sensible.)

• I ask you to shuffle a standard complete deck of playing cards (no jokers) thoroughly. Then I ask for them back (face down). Carefully examining the backs of the cards, I separate them into two piles. I then claim that, through the power of magic, I've made sure that the number of black cards in the first pile is the number of red cards in the second pile! The explanation starts as follows: "While pretending to exmine the backs of the cards, I was simply ..." Can you complete this explanation?

- How many red cards total are there in the deck? Black? So how many red cards in total are there in any two split piles of the complete deck? How does that relate to the number of black cards among the split pile?

- For two piles of cards of size (a) and (52-a) what are the possible values for the difference in the number of red cards in one pile versus the number of black cards in the other?

• As part of a strategic defense proposal, a prominent politician proposes to place a defensive satellite in geostationary orbit directly over Washington DC. What's wrong with this proposal?

- geostationary orbits are only stable around the equator.

• A satellite in geostationary orbit appears to be in the same place in the sky all the time, because the satellite orbits the Earth at the same rate as the Earth rotates. And yet, every satellite in geostationary orbit goes around the Earth with respect to the stars once every 23 hours, 56 minutes and 4 seconds (give or take a few seconds), NOT 24 hours. How, then, can the satellite appear to be in the same place all the time?

- One rotation around the sun must be subtracted every year (imagine that the earth did not rotate at all -- then moving it in an orbit around the sun will still cause a single relative rotation.)

• What is wrong with the idea at this site?

- Numerous classical time travel paradoxes come to mind.

1. Why not wait until the time traveller decides to give you the payout *before* you contribute to the fund, so as to reduce the investment risk to exactly 0, rather than just $10?
2. In what currency (in 500 years) would you expect to be paid in? What bank today would accept that currency? Of course you'd have to transfer it to something like gold. But you would have to *BUY* that gold in the future *BEFORE* travelling back in time. So the question is, taking inflation into account, how much more buying power will $100,000,000.00 have the versus $10 today? If you still think it will be ahead, go look at the greek currency versus what it was worth 500 years ago.
3. What business (let alone bank) would survive for 500 years without having fallen into receivership (thus triggering a degraded payout of accounts, where "dead accounts" would be deprioritized and likely never paid out)? Recessions and depressions happen, and corporations and banks are victims of them.
4. Opportunity payouts are far better than just compound interest. I.e., why not just come back with a list of winning lottery numbers, or las vegas wagering outcomes or just a chart for some volatile stock? Who cares about an initial $10 investment?
5. The net result of this is supposedly to make "free money" on top of your $10 investment. Could not a similar technique be used to arbitrarily increase the supply of any particular thing (such as oil -- i.e., just bring back a future supply to increase our current stock pile, and repeat the process as desired)? Wouldn't our very notions of our economic system be completely turned upside down by such an ability -- I mean to the point of rendering the very concept of money useless?

Mathematical

Set #6

• Consider the following scenario. After waiting 1 second, two balls are placed in a bag, and one of the balls is immediately removed and set aside in a pile. Then after 1/2 seconds another two balls are placed in the and again one ball (from the bag, not necessarily from the two balls just placed) is immediately removed. This sequence is repeated after waiting 1/4, 1/8, ... etc. seconds. The question is, after 2 seconds, how many balls are in the bag? At any stage the number of balls in the bag is always equal to the number pulled out, so it would seem that there should be two infinite sets of balls -- thus there are an infinite number of balls in the bag. However, suppose we label the balls in the order in which they are placed in the bag, and remove them in exactly the numeric sequence of their labelling. Then the set of balls put into the bag are labelled {1, 2, 3 ...} but the balls taken out and sitting in the pile to the side is the sequence {1, 2, 3 ...}. That would suggest that every ball that goes in, eventually comes out.

  In other words, 0 = infinity. Explain what has gone wrong.

- Consider the labeled balls, in which only the even numbers are thrown out until some fixed index k is reached, then the balls labeled k or greater are removed in their numerical order.

- After n steps (i.e., at 1+2^-n seconds), let f(n) be the minimum label of the set of the balls in the bag. Let g(n) be the number of balls in the bag. g(n) = n, however does f(n) converge in any sensible sense?

• Lambert's W function is defined as follows: W(x)e^W(x) = x. Prove that lim_x->inf W(x) / (ln(x) - ln(ln(x))) = 1.

- What is W^-1(ln(x)-ln(ln(x)))?

• Suppose you are in the elevator of a 20 story building at the top floor. All of a sudden the elevator cable snaps, and the emergency brake completely fails (an insanely unlikely occurence) and the elevator proceeds to drop in a 20 foot free fall. If you do nothing, the fall will kill you, so before the point of impact you consider possibility of jumping up from the floor of the elevator as hard as you can right at or possibly just before the point where the elevator finally hits the ground. Does this have any chance of working?

- How does one measure the energy of the impact that is transfered to the elevator and ultimately you the occupant?

- What is the maximum speed that a person can travel at as a result of jumping? Compare this to an accumulated speed of free falling for 20 floors.

• Suppose a bucket is floating in a bathtub filled with water, and in the bucket is a metal wrench. Now suppose we take the wrench out of the bucket and drop it into the bathtub so that it sink and is completely submerged. Does the water level in the bathtub raise, lower, or stay that same?

- If an object sinks, then what is its density compared with water?

• Suppose 100 prisoners are in a line. Each prisoner is given a hat, but are not allowed any form of communication after they are given the hats (no blinking morse code or anything like that). They are standing in a line facing front and can see all the hats of the others in front of them, but not their own or anyone behind them. They are told that the probability of the hat they are wearing being black is 2/3, and that the remaining hats are white and that each hat was independently randomly chosen with these odds. Now each prisoner will be called up in the order of the line starting with the one in the back (who can see 99 other hats in front of him/her), one by one is forced to guess which color the hat on their own head is. If they guess correctly they live, if they guess incorrectly they are executed on the spot right then and there. As the procedure progresses the others can hear the guesses of those behind him/her and whether or not they guessed correctly.

  Ok, assuming that the prisoners are allowed to collude and strategize before they are given their hats (they know of the pending situation before it takes place, but cannot communicate at all once the hats are given out), what should they do to maximize their probability of their own survival? What should they do to maximize the number of surviving prisoners (is this the same question)? And assuming there is a difference in the two strategies, what if some of the prisoners (with probability p) decides to be selfish and go with a selfish strategy instead of strategy which maximizes the number of survivors?

- If a prisoner were being selfless for the benefit of others, he/she could use their guess as a binary communications mechanism instead of a genuine guessing mechanism.

- If each guess only told exactly enough information for the next person to know their hat color, then this strategy could only be used once (one person projects the information forward, and one person receives the information).

- Some set of prisoners must give information about all the prisoners.

- What is exactly the difference in knowledge about all the prisoners between the first and second prisoner to have to guess? What is the most minimum way of encoding this difference in knowledge, in a way that the *difference* between these two sets of knowledge is known to all the prisoners who hear guesses?

- Suppose the first prisoner asked simply gives information whether or not a count of the number of white hats he/she sees is even or odd? Note that this strategy is independent of the actual number of prisoners.

- This second strategy will save everyone deterministically except possibly the first person, who basically has a 50% chance of guessing wrong and dying; so a 99.5% success rate. The greedy strategy basically has a 66.6% success rate. The optimal strategy (from either the selfless or selfish point of view) is to be part of the second strategy, if possible, though it might be out of your control. So lets consider the third case where some prisoners might be selfless, and some selfish.

- As soon as a prisoner can established that some deterministic previous prisoner has given the parity of the number of white hats he/she sees ahead, they can assume they the other prisoners before him/her knows at least as much, and have switched to the selfless strategy thus guaranteeing their own survival.

- How would any given prisoner interpret the possibility that a previous prisoner guessed their color as white and survived? Does a sequence of black guessers and surivivors tell them anything? What if someone prior to them has guessed white but guessed wrong?

Set #5

• An enemy submarine is travelling along a ruled line starting at an unknown integer offset at time 0, and moving at an unknown constant speed of a integer displacement per minute. Now suppose we have a missile system with unlimited ammunition that can strike at any single integer offset on this line at any given moment. Is there a way to strike the submarine with a missile in a finite amount of time?

- Create a well defined infinite list L of integers pairs (x, y) that are an exhaustive list of all integer pairs.

- At time t launch a missile at the position x(t)*t+y(t), where (x(t),y(t)) is the entry of the list at position t.

• 400 pirates plunder a ship and gain 100 gold coins. Now they must split the coins among them. To do this, they always follow this procedure: One pirate makes a proposal about how to split the gold. Then they all vote whether or not to accept this distribution of the booty. If the proposal takes at least half (not half+1) the votes then the proposal passes, the coins are given as the proposal says and they are done. But if the proposal fails the vote, then the stupid pirate that made the proposal is killed, and the next one makes his proposal (they all know their turn a priori, that is to say there is a ranking amongst them.) Dead pirates don't vote. Now, every pirate has the same criteria when voting for or against a proposal : 1) He must do what he can to live, 2) If he is sure he'll live, than he tries to take as many gold coins he can and 3) If the first 2 criteria are satisfied, then he tries to kill as many of the other pirates he can. A gold coin can't be cut in pieces and all these pirates are logical enough to make the right decisions and they all know that about each other. What is the most logical way for the gold coins to be split, and how many pirates survive this ritual?

- Suppose there were only two pirates, what would the first pirate to speak propose?

- Suppose there were three pirates, what would the first pirate to speak propose (in lieu of the above)? I.e., if his proposal was defeated what would it mean for the last pirate to speak?

- Suppose there were 200 pirates? Write down the proposal as determined by the pattern established in the above two scenarios. Now is there anything special about the case of 201 pirates (how much does the proposing pirate suggest taking for himself)? Is 202 pirates different? Now suppose there are 203 pirates. Is it possible for the proposing pirate to get 102 votes? How much does it cost to get the vote of someone who will next speak if he knows for sure his proposal will be voted against?

- Now do the cases of 203, 204, and 205 pirates. Now be careful, 206 and 207 pirates does not follow the expected pattern -- a new pattern emerges. 208 pirates is different.

- What happens in the case of 216, 232, 264, and 328 pirates which does not happen in the other cases above 208?

- Suppose there was 1 coin and between 2 and 18 pirates. The following table shows the outcomes:

\

Pirate #

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

2

0

1

3

1

0

0

4

0

1

0

0

5

*

*

*

*

*

6

1/3

0

1/3

1/3

0

0

7

*

*

*

*

*

*

*

8

*

*

*

*

*

*

*

*

9

*

*

*

*

*

*

*

*

*

10

0

1/3

0

0

1/3

1/3

0

0

0

0

11

*

*

*

*

*

*

*

*

*

*

*

12

*

*

*

*

*

*

*

*

*

*

*

*

13

*

*

*

*

*

*

*

*

*

*

*

*

*

14

*

*

*

*

*

*

*

*

*

*

*

*

*

*

15

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

16

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

17

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

18

1/7

0

1/7

1/7

0

0

1/7

1/7

1/7

1/7

0

0

0

0

0

0

0

0

Each row shows essentially the best proposal for each pirate for the given number of pirates (shown in the leftmost column). The proposing pirate is the right-most entry. Green boxes show pirates that vote for the proposal. Light red boxes are votes against the proposal. Yellow boxes are possible votes, conditional on some probability. If the count box is white, then the proposal is accepted, and all pirates survive. If the count box is red, the proposal fails and the proposing pirate is killed. In the main box, a value of 0 means that in the proposal no gold is given to the pirate that corresponds to his rank (which corrsponds to the column index.) A value of 1 in the main box means that the 1 gold coin is proposed to go to that pirate. A fractional value means that the gold piece will be proposed to go to that pirate with that given probability. A * in the main box means that it does not matter what proposal is made.

Each row of the table is created inductively. That is to say, the prior rows are considered to show the best outcome, and the proposal and votes of each generated row takes the 3 rules into account as well as the prior rows to maximize each pirate's outcome. So for example, the first interesting case is row 6. Here pirate #6 (the proposing pirate) votes for his own proposal because of rule 1, pirate #5 also votes for the proposal because of rule 1, because he sees that he will die for sure if he is forced to propose (see row 5, where it shows that all proposals will fail) and then the proposal will give the gold coin to one of pirates 1, 3 or 4 corresponding to the pirate who will also vote for the proposal giving the required 3 votes for the proposal to pass. The reason why this proposal is optimal is because it is the only and cheapest way to obtain 3 votes -- he (the proposing pirate #6) buys one vote, and relies on his vote and the vote of pirate #5. Note that if his proposal had been to pirate #2, it would fail because pirate #2 would use criteria #3 to vote against the proposal knowing that the next proposal will also fail and that he will obtain the gold coin on the proposal by pirate #4 (thus increasing the number of killed pirates by two without risking his own life or decreasing his share.)

When there are between 7 and 9 pirate inclusive, its possible for the proposing pirate to try to bribe one of the pirates between #1 and #6 inclusive, however it will not change the outcome since at least 5 of those pirates will vote against the proposal. Pirates #7 through #9 inclusive basically are facing certain execution in these situations, and so are eager to vote for any proposal that will stop the executions (assuming some sort of futile desperation on the part of the pirate). But when there are 10 pirates, there are only 5 who are certain to vote against the proposal. The 10th pirate can count on his own vote, the three votes of pirate #7, #8 and #9 (who would otherwise face certain death) as well as one vote from one of the pirates #2, #5 or #6 who can be bribed with the coin. Note that if pirate #10 tries to bribe one of pirate #1, #3 or #4 they actually might still vote against the proposal because they might have a collusive relationship with pirate #6 which ensures them the gold coin anyways (so choosing #2, #5, or #6 is the only way to be sure to get their extra vote.)

• What has gone wrong here:

  √

  -1

  =

  √

  1  -1

  =

  √ 1 √ -1

  =

  1  √ -1

  =

  1  √ -1 √ -1 √ -1

  =

  √ -1   -1

  =

  - √

  -1

• Suppose we have a sequence of n integers {a₀, a₁, ... a_n-1} each from the range [0, 2ⁿ-1]. Give a simple function that returns a specific integer in this range which in not equal to any of the a_i. (Computer programming interpretation: write a function using just arithmetic and logic operation which do not use control structures like "if" or C's "? :" operator or Perl's "when" clause or loops.)

- ~((a₀ & 1) | (a₁ & 2) | ... | (a_n-1 & 2^n-1)), that is to say the nth bit of this expression is the logical not of the nth bit of a_n.

• Does there exist a real valued function that grows faster than any polynomial but not as fast as any monotonically increasing exponential? If so, give an example of such a function. That is to say, find a function f(x), if it exists, such that:
  • For all integers n > 0, there exists an X such that f(x) > xⁿ for all x > X.
  • For all real values e > 0, there exists an X such that (1+e)^x > f(x) for all x > X.

- In the above construction try O(g(x)) > constant and h(x) a polynomial.

- Try f(x) = x^ln(x)

Set #4

• The band U2 whose 4 members are Bono, Edge, Larry and Adam need to get to the stadium to perform. On the way there they encounted a bridge that they need to cross to get there. But its pitch black out, they have one flashlight, and the bridge can only support two at a time. Its too treacherous to cross the bridge without the flashlight, so no journeys across the bridge are made without the flashlight. Now they are in kind of a hurry, so they need to get across as fast as possible. It turns out that they walk at different speeds. By themselves Bono, Edge, Larry and Adam can cross the bridge in 1 minute, 2 minutes, 5 minutes and 10 minutes respectively. So if two are walking across, their combined speed is that of the slower of the two. The question is, how can they cross the bridge, and how do they do it in the least amount of time?

- Is 19 minutes a particularly difficult or unique answer to arrive at? How many ways are there of acheiving 19 minutes?

- There is no escaping the fact that Adam will require 10 minutes to get across and therefore it must be assumed that at least 10 minutes will be taken just geting him across. Is the same true, therefore, of Larry?

• * Just for fun a gambler approaches you and asks you if you want to make an even bet with him. Sure you say, being a gambler yourself. Now he says he's going to pick two different random numbers from a distribution not known to you. He will then write the two numbers of two small pieces of paper and put each one in each of his enclosed hands. You then pick a hand and he will reveal the number in that hand. You then place your money on which hand you think contains the larger number. He will match your money, betting on the other hand, the numbers will then be revealed and whoever was right keeps the sum of the money. You only get one shot at this, and the bet is $10,000. The question is, is there a strategy to beat 50:50 odds and if so how?

- Suppose the distribution was the normal (or guassian, as some universities call it) distribution with mean m, and standard deviation s, and was known to you before hand. How would you try to exploit this information? What about any other continuous, and known distribution?

- If the numbers are completely random from your point of view, then you too can chose undisclosed random numbers which may have certain statistical properties with respect to the gambler's chosen numbers.

- Before the gambler shows the first number, randomly choose a secret random continuous monotonic distribution of the real numbers (so that the probability of chosing any particular number is 0, but the probability that a chosen random number is in any particular range is always greater than 0). Then chose a secret random number with that secret random distribution. Then look at the number he exposes (chosing your secret random distribution and secret random number from that distribution before you look at the exposed number is kind of important from a bias point of view) and chose it if it is larger than the secretly chosen number, and switch to the other hand if it is smaller. Does such an algorithm improve your odds?

- The algorithm above does improve your probability of winning because the probability that the two numbers surround the secret number you chose is non-zero.

• A duck is swimming in the center of a perfectly circular pond, and a fox is on the land at the very edge of the pond. The fox is hungry and wants to eat the duck, but it cannot swim. The duck wants to get out of there but needs to reach land in order to be able to fly away. If the duck swims at 1 meter per second, and the fox can run around on land at 4 meters per second, can the duck somehow escape?

- Suppose the duck swims in concentric circles about the center. What is the maximum radius circle that it can swim about in while being able to dictate the angular difference (relative to the center) between the fox and itself?

• Explain this:

  

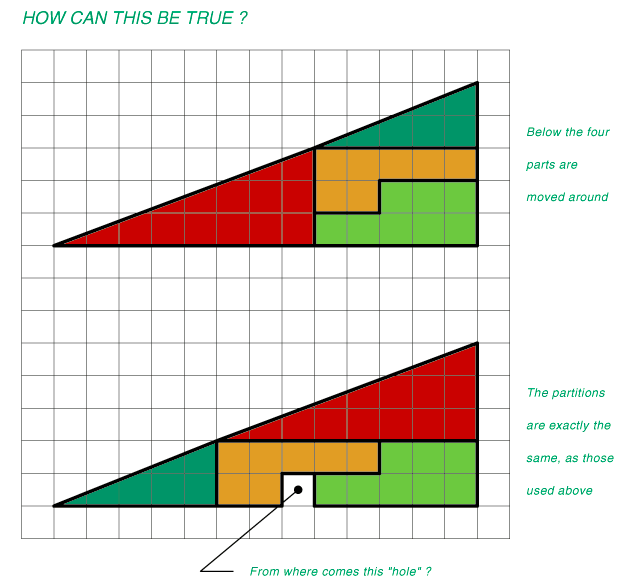
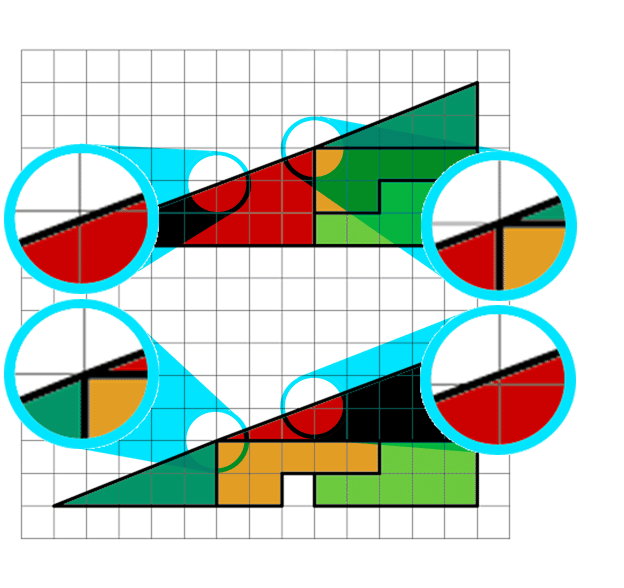
- If we were to flatten and stretch a 1x1 (platecine) rectangle into parallelogram of base √29 and height 1/√29 (about 0.185695...) with the top shifted over by √73 (so the thin angle is about 1.245... degrees) and you placed it along the diagonal, of the triangle without the hole, would it fit? Would it be easily visible?

• Create a directed network on 10 vertices such that the path length between any two distinct points is at most 3, and each vertex has at most 2 outgoing connections.

Set #3

• Suppose we have a uniformly random input bit stream that we do not allow more than five 1 bits in a row to be output. To ensure decodeability we use the following scheme: we simply copy the input bits to the output bits, and as soon as the output stream receives five 1 bits in a row an additional 0 bit is sent. Under this scheme what is the expected asymptotic percentage change in the length of the stream from input to output?

- The answer is not 1/32 or 1/31 (as a ratio)

- The typical incorrect answer of 1/32 is usually arrived at under an incorrect assumption of independence. Stay away from this style/line of reasoning altogether. Remember that uniformly random choices are essentially ratios of the size of a sets. Look at the size of sets, and generate the probabilities afterwards as a side effect.

- Consider an infinitely long stream of uniformly random 1's and 0's (our input) and break it at some point. What are the odds that up to that point the sequence was 0... ? What are the odds that up to that point the sequence was 10... ? 110... ? 1110... ? and so on? Which of these sequences causes the additions of a single extra bit in the output corresponding to the breakage point?

- Remember that if -1<a<1 then 1 + a + a² + a³ + a⁴ + ... = 1/(1-a).

- Take a look at experimental results.

• Suppose we have a pair of lines in regular 3 dimensional space and a pair of line segments of length a and b on the lines (one on each.) By joining all the vertices of the line segments we get a pyramid. In fact, if the lines don't intersect you will have a pyramid of non zero volume no matter where on the lines the line segements are placed. What positioning of the line segments maximizes the volume of the pyramid?

- The volume of the pyramid for any particular positioning of the lines can be expressed as the difference in volume of two pyramids who's volume is easy to calculate.

- Think of the volume as being proportional to certain lengths, vector dot products and so on.

• Suppose we have 100 lockers which start all closed. You start at one end and open every locker one by one. You then return to that end and then starting with the second locker close every other locker. You then return to that end again and starting from the third locker change the state (if it is open close it, if it is closed open it) of every third locker. Then every fourth, every fifth and so on. You do this for 100 passes. What is the state of each locker after you are done?

- Forget the first pass, and consider the subsequent passes.

- For each locker, which passes will actually intersect with that locker?

- Which numbers have an odd number of factors, and which have an even number?

• Suppose we have n coconuts gathered by 5 primitive men that have agreed to share them equally but who do not trust each other. They all go to sleep, but in the middle of the night the first guy wakes up divides the coconuts by 5 and hides his share of one fifth in his hut but there was a remainder of one coconut left after division so he gives it to a monkey that happens to be around (and awake) then he goes back to sleep. The second guy wakes up and divides the remainder of the pile into 5 and hides his share, but again there was a remainder of one that he gives to the same nearby monkey (which is still awake) before going back to sleep. This same procedure occurs for each of the remaining 3 primitive men (including the last one because nobody was a aware of the others' insomnia.) Assuming that the monkey gets 5 coconuts (there was always a remainder of 1 after dividing the piles by 5) what is the minimum number of coconuts that they could have started with?

Hint 1: Let the starting number of coconuts be p₀. After the ith primitive has taken his share and given one to the monkey let the number of remaining coconuts be p_i. Each p_i must be a positive integer. For i=0,...,4 then we have the following relation:
  4 * (p_i - 1) / 5 = p_i+1

Hint 2: 4 * (p_i - 1) / 5 = p_i+1 is equivalent to saying:
  4 * (p_i + 4) = 5 * (p_i+1 + 4)

Hint 3: Let q_i = p_i+4. Then q_i+1/q_i = 4/5. This solves to q_i = k * (4/5)ⁱ, for some value k.

Hint 4: So p_i = k * (4/5)ⁱ - 4. But each p_i is an integer, so k * (4/5)ⁱ is an integer for i=0,...,5. This means k, 4*k/5, 16*k/25, 64*k/125, 256*k/625 and 1024*k/3125 are all integers.

Hint 5: If k is an integer and 4*k/5 is an integer, then k is divisible by 5. Furthermore, if 16*k/25 is an integer, then k is divisible by 25. Continuing this reasoning we can conclude than k may be any multiple of 3125 to satisfy the requirement that each p_i is an integer.

Solution: Let k = 3125*t. Then p_i = 3125 * t * (4/5)ⁱ - 4. If t <= 0 then p_i < 0, but p_i are all positive, so t must be positive. If t is positive, then p₀ is minimized at 3121 by t = 1. Checking the rest of the sequence of p_i we see: p₁=2496, p₂=1996, p₃=1596, p₄=1276, p₅=1020 which are positive integers. So the answer is 3121.

• Suppose you and nineteen other fine up standing citizens are captured by terrorists and each of you is put into an room (isolated from the others) with a button and a timer which is counting down starting from 10 minutes. You are told that if you press the button you will die instantly, but everyone else who does *not* press the button will be allowed to live and set free, however, if noboy presses the button, everyone will die. Given that the terrorists will keep their word, how would you decide on whether or not to press the button?

- There is a little bit of psychology going on in this question.

- Take the point of view of finding an algorithm which maximizes the number of saved lives that will be saved and assume that you could have pre-emptively communicated this to the other 19 civilians.

• Out of the set of integers 1,...,100 you are given ten different integers. From this set, A, of ten integers you can always find two disjoint non-empty subsets, S & T, such that the sum of elements in S equals the sum of elements in T. Note: S union T need not be all ten elements of A. Prove this.

- How many possible subsets of 10 distinct integers are there?

- What are the minimum an maximum possible sums for the 10 integers?

- If two of the subsets s and t are overlapping sets then (s-(s&t)) and (t-(s&t)) are disjoint sets with the property that s and t have the same sum if and only if (s-(s&t)) and (t-(s&t)) do.

Set #2

• A boy, a girl and a dog go for a 10 mile walk. The boy and girl can walk at 2 mph and the dog can trot at 4 mph. They also have a bicycle which only one of them (including the dog!) can use at a time. When riding, the boy and girl can travel at 12 mph while the dog can pedal at 16 mph. What is the shortest time in which all three can complete the trip (and how do they do it)?

- Hint not yet available.

• Four bugs are placed at the corners of a square. Each bug walks always directly toward the next bug in the clockwise direction. How far do the bugs walk before they meet?

- What 2 dimensional geometric shape is alway formed by the coordinates of the four bugs taken in a consistent order?

- At what speed is each target bug travelling away from the bug that is chasing them?

- Consider an approximation of an initial part of the path taken as depicted by the stright line between the two blue dots in the diagram below.

Notice that the four bugs are still at the 4 corners of a (smaller) square after each takes the same analogous symmetric step.

- From the diagram above, assume that these partial paths are taken recursively in proportion to the size of the square that the 4 bugs outline. If the total path length is T, then

    T = sin(θ) + (cos(θ)-sin(θ))*T

Which solves to

    T = sin(θ)/(1-cos(θ)+sin(θ))

Now argue that as θ -> 0, the initial path step will more closely approximate the real initial displacement for that same length. Then compute lim _{θ -> 0} T.

• Suppose you had an infinite supply of equally sized, rigid, playing cards. You pile them on the edge of a table by placing them one by one on top of each previously placed card (each also only touching the previously placed card) so as to have the total structure lean as far off the edge as possible without any other support (besides themselves and gravity) and without falling off the edge. If you are further subjected to the restriction that each card only touches the previously placed card and that you may not disturb any card if subsequent cards have been placed, how far over can you go?

- Add the cards to the bottom of the stack instead of the top.

- What is the taylor expantion of ln(1+x)? What is ln(0)?

• In trapezoid ABCD, with AB parallel to CD, M is the midpoint of AD. Find the ratio of the area MCB to the area of the trapezoid ABCD. (from Mayhem)

- Hint not yet available.

• A triangle with inradius r and area K are given. Prove that 9r*r/K <= tan(A/2) + tan(B/2) + tan(C/2). (from Mayhem)

- Hint not yet available.

• Suppose you have milk and coffee in equal quantities in two different cups. You pour some of the milk into the coffee then pour back some of the mixture back into the milk cup so that there is the same total amount of liquid in both cups once again. Is there more, less or an equal amount of milk in the coffee cup than there is in the milk cup?

- The "mixing" is a red herring. Pretend the substances don't mix, since mixing doesn't affect the volume. Then there are 4 "portions". What are the constraints on these four portions?

Set #1

• Let's say we (you and me) play a simple game. I have a circular table and an unlimited supply of identically shaped Cuban cigars. We each take turns placing a cigar on the table without disturbing any other cigars already there in the process and without overlapping any pair of cigars. The winner will be last person to successfully place a cigar on the table subject to the given restrictions. If I give you the option of going first, how would you play in order try and win?

- What are the features of a circle and how does this dictate your first move?

- Clearly any strategy is HIGHLY dependent on how I respond to your moves.

• I know 3 psychics. A fair coin is flipped and then hidden. Molly has an 80% chance of guessing the state of the coin (heads or tails), Spike has a 70% chance, while poor Waldo only has a 10% chance of a correct guess. What is the best scheme using all of these guesses to predict the state of the coin? What degree of accuracy does the best scheme give?

- Just how effective is Waldo?

- What are the chances they all agree and are wrong? What are the chances they all agree and they are right?

- There's no reason not to do this with brute force (especially if you use a spread sheet program, such as Open Office's Calc program):

Spike	Molly	Waldo	Coin	Probability	Winning strategy
H	H	H	H	.7*.8*.1*.5 =  2.8%	if all equal, go with consensus
H	H	H	T	.3*.2*.9*.5 =  2.7%
H	H	T	H	.7*.8*.9*.5 = 25.2%	if not all equal invert waldo
H	H	T	T	.3*.2*.1*.5 =  0.3%
H	T	H	H	.7*.2*.1*.5 =  0.7%
H	T	H	T	.3*.8*.9*.5 = 10.8%	if not all equal invert waldo
H	T	T	H	.7*.2*.9*.5 =  6.3%	if not all equal invert waldo
H	T	T	T	.3*.8*.1*.5 =  1.2%
T	H	H	H	.3*.8*.1*.5 =  1.2%
T	H	H	T	.7*.2*.9*.5 =  6.3%	if not all equal invert waldo
T	H	T	H	.3*.8*.9*.5 = 10.8%	if not all equal invert waldo
T	H	T	T	.7*.2*.1*.5 =  0.7%
T	T	H	H	.3*.2*.1*.5 =  0.3%
T	T	H	T	.7*.8*.9*.5 = 25.2%	if not all equal invert waldo
T	T	T	H	.3*.2*.9*.5 =  2.7%
T	T	T	T	.7*.8*.1*.5 =  2.8%	if all equal, go with consensus
Totals:				100.0%	90.2%

• (Watch out, this question is very controversial.) On the game show "Let's make a deal", Monty Hall (the host) walks up to a contestant and gives them $100 unless they want to play "the three doors". They usually turn down the money and play "the three doors". Now behind one of the doors is an enourmous cash prize, behind the other too are silly prizes such as a years supply of toilet paper or a goat. So Monty asks this same contestant to pick a door, which they do. Then, before opening the chosen door and revealing what's behind it, he opens one of the other doors which reveals one of the lesser prizes. Monty then gives this contestant the option of staying with their chosen door or switching to the other door which still remains closed. The contestant then decides what to do and is rewarded with whatever prize is behind the door they finally chose. So the question is, should the contestant switch or stay?

- Suppose there were 100 doors with 1 prize and Monty opened 98 of them to reveal nothing after you picked your door ...

• Extended Monty Hall Suppose that Monty has the option of not offering you the opportunity to switch and further suppose that you do not know beforehand whether or not Monty will offer to switch. Ok, the show is on a budget so Monty's primary objective is to not increase your odds of winning with his strategy versus any counter strategy you might come up with. But Monty's secondary objective is to make the game as entertaining as possible by offering the switch as often as possible without compromising his primary objective. The question then is, what is Monty's strategy, and what is your best counter strategy?

- Draw a tree diagram of all the possible events that can occur. Realize that there are only three decisions that are made (two of the decisions are the same from a certain point of view) and assign probabilities to the possible choices.

- For a fixed p,q, how does one maximize the expression (1 + r*(2*p-q))/3? How does it depend on that values of p and q?

• Let's you and me play another game. This one is simple enough, tic-tac-toe n in a row. n is an integer greater than 1 and we'll play on an unbounded 2D grid, following the regular rules of tic-tac-tow. I allow m in a row, where m>n, to be as good as n in a row, i.e., you still win even if you get too many in a row. For what n can the second player force a win? (Hint/Note: It has been proven that tic-tac-toe 8 in a row is a draw, with best play from both sides.)

- If tic-tac-toe 8 in a row is a draw, what about 9 is a row?

- Do question 1 first.

- If the second player had a winning strategy, how should the first player try to play?

• Ok, enough of these games. There are three people named Larry, Curly and Moe. One always tells the truth, one always tells a lie and the other gives unpredictable answers, but all of them can only answer yes or no questions (with yes or no). Like any classic Smullyan puzzle (from whom I believe this problem originates), the goal is to ask a certain number of questions to figure out who is who. In this case, the three know who is which and now you are allowed three yes or no questions (each directed to only one of the three at a time) to figure it out for yourself. How's do you do it?

- Although a single question and answer cannot precisely determine the identity of a single person, the right question can eliminate a possible identity.

• Let's say you have a table with 4 perfectly even table legs arranged in square positioning. I.e., on a flat floor the table sits perfectly flat. Now lets say that you have a floor that isn't quite flat. When you first place the table on the ground it wobbles because not all the legs touch the ground at once. Suppose that the floor is essentially unbounded and that from any given position you can drag the table in any direction (possibly requiring that you tilt the table so that only two of the legs are touching.) Can you always find a position on this floor such that the table does not wobble?

- If you dragged the table around on 3 legs (with the 4th up in the air) all over the place it would seem that nothing could be done if the 4th leg always stayed in the air.

Back to the puzzles